实验的基本假定

n        晶体基本结构单元——质点

n        X-射线束——方向性足够好

n        由Bragg公式 2d sin( q )= l , 每个晶面族对应底片上一个laue斑

 

定性分析

n        X-射线束有一定的发散度，本身也有一定的强度分布

n        晶体结构单元有一定的形状、大小，并且晶体本身存在 absorption, extinction , distortion, imperfection

n        照相底片本身的影响

半定量分析

Laue 实验装置作如下

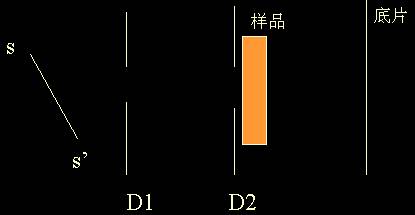
整套实验装置包括：X-射线源（ss’）, 准直系统（D1、D2）, 样品, 底片

 

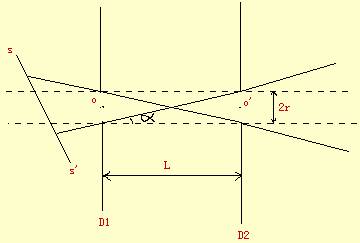
D1、D2作为中心对准的圆孔，孔径为2r, 两屏间距L>>2r,

tan(a) = 2 r / L

则X-射线束发散角:

2 a ≈ 4 r / L          (1)

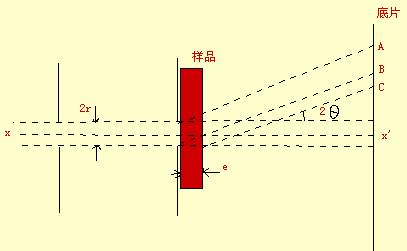
n        简化假设

=      晶体紧靠准直屏D2

=      晶体尺度要能覆盖整个准直屏

=      晶体内晶面与纸面垂直

=      简化实验装置图

=      底片上laue斑小:

AC = AB + BC    = 2 r + e tan( 2q )          (2)

n        对（2）式的若干讨论

每一个laue斑都由三部分衍射光汇合而成，考虑图中A、B、C、三束衍射光，对应晶体不同厚度，laue斑将有不同结构，晶体不同厚度将影响衍射角的测量，改进方法：利用A束衍射光，考虑 tan(2θ)<=2 r / e , 此时laue斑中心有衍射光重叠，中央比边缘强度大

简化实验装置图

l        X-射线进入晶体的一层衍射光

l        X-射线在晶体中的衍射光  

l         X-射线离开晶体的一层衍射光

 

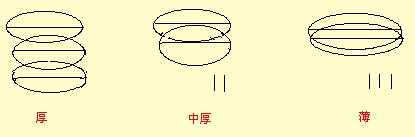
半定量分析结果之应用——不同情况下摄得laue相大致图象

n        实验基础：所用X-射线实为具有不同发散或汇聚程度的射线束的集合

n        假定：样品无限薄

n        结果：laue斑决定于射线束的发散或汇聚情况，以及射线束和晶体的作用面积。包括以下６种情况：

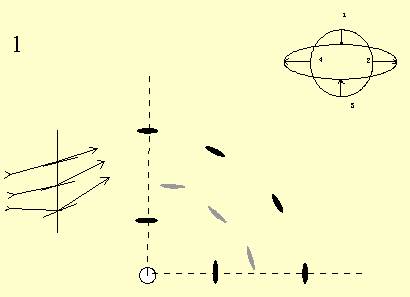
Conic divergence, large surface of illumination

 

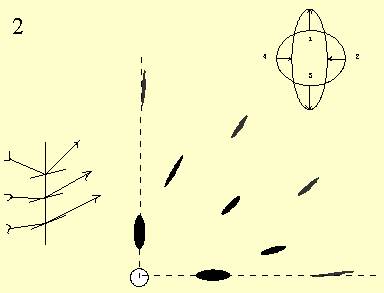
Conic convergence, large surface of illumination

 

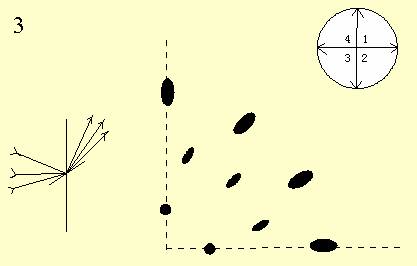
Conic convergence, point-like surface of illumination

 

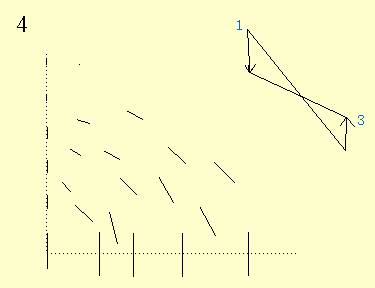
Linear divergence, large surface of illumination

 

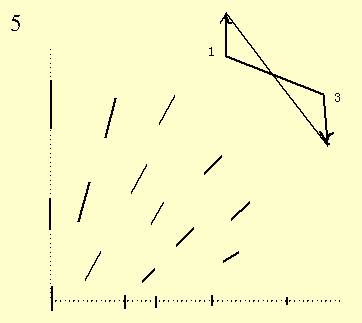
Linear convergence, large surface of illumination

 

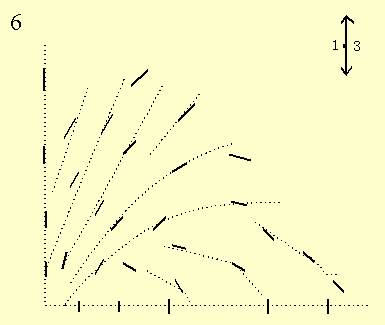
Linear convergence, point-like surface of illumination